did-交叠did-模糊did
什么是政策评估？
一个政策效应评估是对可以归因于某项具体项目、政策的，对个体、家庭、团体或公司的社会福利变化进行评价。
政策评价的中心问题是，如果那些接受干预的人实际上没有接收这个项目，他会发生什么？
一、DID方法
DID处理选择偏差的基本思想：允许存在不可观察因素的影响。
DID政策效应评价结合了前、后，参与和未参与两个方面的影响。
*由此产生两个问题：*（1）选择偏差和（2）时间偏差
1.DID估计量
| 处理 | 对照 | |
|---|---|---|
| 政策前 | ||
| 政策后 |
DID估计的假设是，在没有政策的情况下，个体i在t时期的结果为：
1.选择偏差与个体的固定特征（
2.时间趋势项（
这个两个识别假设的必要条件合起来被称为共同趋势假设。
在没有政策影响下，个体i在t时期的结果为：
时间趋势：
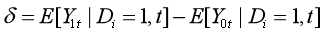,其不依赖于时间和i的个体特征。
处理组结果：
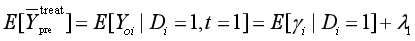
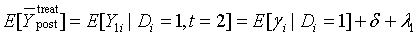
计算前、后的估计量，则有
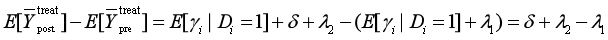
计算对照组、处理组的估计量，则有
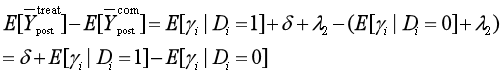
DID估计量消除选择偏差、时间趋势：
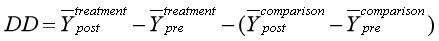
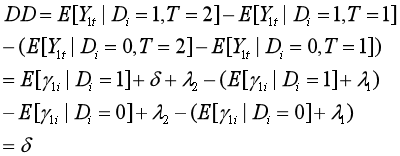
即政策的真实影响。
2.常用估计命令的结果比较：
| Reg（截面堆积） | Xtreg | Arcg | reghdfe | |
|---|---|---|---|---|
| 个体固定效应 | i.id | ,fe | ,absorb(id) | Absorb(id time) |
| 时间固定效应 | I.time | I.time | I.time | Absorb(id time) |
| 估计方法 | OLS | 组内去平均后OLS | OLS | OLS |
| 优点 | 命令熟悉简单 | 固定效应官方命令 | 官方命令，可以提高组别不随样本规模增加的估计效率（大样本分类变量多） | *高维*固定效应模型，可以极大提高估计效率。且支持多维聚类和多重固定 |
| 缺点 | 速度慢，结果繁杂 | 需要手动添加时间固定效应 | 需要手动添加时间固定效应 | |
| 使用频率 | 较少，多用于比较 | 较多 | 较少 | 较多 |
其他还有：
Diff didregress xtdidregress
检验
1.平行趋势
2.安慰剂检验
2.1关于政策实施时间的安慰剂检验
2.2关于处理组的安慰剂检验
二、多期DID（渐进DID、交叠DID）
传统DID一般针对政策实施时点为同一时期，但是有时会遇到每一个个体的政策实施时点不完全一致的情况，这个时候需要考虑政策效应的异质性（ddid csdid）。
多期DID的关键在于，处理期虚拟变量的构建，因个体而异，可以写作postit（即依赖于个体i，又依赖于时间t），此时称为渐进DID
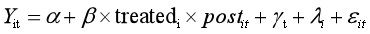
假设一个五期面板数据:
第一个个体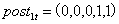
,第二个个体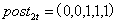
分别意味着，第一个个体在第4期受到政策冲击，第二个个体在第3期受到政策冲击。
也可以写为以下形式：
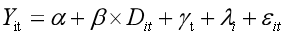
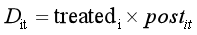
三、广义DID
无论是传统DID还是交叠DID均假设存在处理组和控制组的区别，但有时某项政策在全国范围内统一铺开，此时没有控制组，只有处理组，就要考虑广义DID。
使用广义DID的前提是，虽然所有个体均同时受到政策冲击，但政策对于每一个个体的影响力度并不相同。此时政策Di用相应水平的连续函数intensityi来构造实验组和控制组。
例如：Bai and jia （2016）使用清朝府级面板数据，考察废除科举制对于革命起义的影响，由于科举制度于1991年在全国统一废除，不存在严格的控制组，但是由于科举配额在各地存在巨大差异，废除科举这个政策实施对于各地的影响力度差别极大。因此这篇文章中以“科举配额占总人口比值”作为intensityi。
钱雪松和方盛（2017）认为《物权法》增加了企业运用担保物权进行融资的操作空间，因此通过固定资产占比构造对照组和实验组。
在操作中，目的是寻找合适的intensityi变量（需要严格的理论推导），作为传统DID中的treatedi虚拟变量。也可以使用连续型变量，有两种做法，一种是按照均值进行分离分为对照组和实验组，另一种直接与time做交乘项作为DID （参考《数字经济发展与企业价格加成》 柏培文，2021）
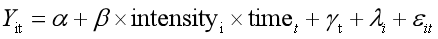
四、模糊DID
传统DID基础设定是：对照组两期都不受干预，而处理组在第一期不受干预而在第二期受到干预。
实际中，这种不受干预到受干预的急剧变化的DID并不一定成立，在模糊（fuzzy）DID中，可能存在没有任何一组显示出来急剧变化（不存在“干净”的处理组），也可能没有任何一组完全未受到干预（不存在“干净”的对照组），此时可以通过模糊DID的手段评估政策效果。
主要包括三种识别策略：分别为Wald-DID、Wald-TC和Wald-CIC。
基础框架：
将第一期未受到干预而第二期受到干预的观测个体称为“转换者”，主要关注的参数就是处理组中转换者的局部处理效应（LATE）。
Y表示观测到的结果，D、G/T为三个0-1二元变量，分别表示是否受到干预、处于对照组/处理中、观察使其为第一期/第二期。
对于传统DID，意味着D=GT，而对于模糊DID，D不等于GT,可能出现的情况包括：对照组中某些个体受到了干预或处理组中一些个体始终未受到干预。
假设1：“模糊设定”
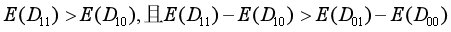
处理组T=1时受干预个体>处理组T=0时受干预个体，处理组的转换者>控制组的转换者，这一设定实质上是规定那些为处理组，哪些为对照组。
假设2：“对照组受干预的个体稳定”
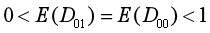
对照组受干预的个体的比例在两期间不变。
假设3：“干预参与方程”
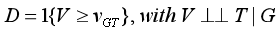
某一个体是否受到干预（的倾向），取决于其所在的组别和观察时期，每组中，*观测个体只能向单一方向转换*。
假设1和假设3意味着任何一个个体只能由不受干预向受到干预转换。
所关注的内容就是这种转换的*局部处理效应，即：*
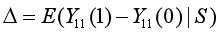
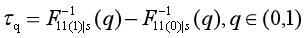
前者即为LATE（处理组中从未接受处理转变为已接受处理的转变者所接受处理的潜在结果），后者为局部分位数处理效应（LQTE），其中S表示转换者，F表示某一随机变量的累积分布函数。
1.Wald-DID
假设4“共同趋势”
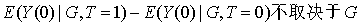
这一假设与传统DID相同，意味着从T=0到1期间，处理组和对照组的不受干预者的结果变化一致。
*假设5*“干预效果在时间上是稳定的”干预不随时间变化而变化
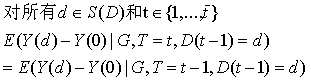
*假设6：*“干预效果在组间是同质的”
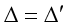
其中，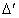
为对照组中转换者S对应的LATE。
*Wald-DID：*如果满足假设1和假设3-5：
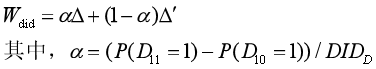
α表示处理组中转换者所占比例与两组转换者比例差距的比，Wald-DID实质上是一个处理组与对照组间加权差值。
如果在此基础上满足*假设2：*“对照组受干预的个体稳定”和*假设6：*“干预效果在组间是同质的”
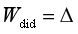
实际上：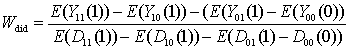
就是两个DID的比，一个是结果Y的did，一个是处理变量的DID
*2.Wald-TC*
Wald-TC实际上是进行了时间修正的估计量，主要是针对假设4：
*假设4（2）：*条件的“共同趋势”
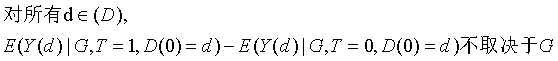
即在*假设4*的基础上，对受干预者的时间趋势进行约束，认为处理组和对照组的受干预者的结果变化也是一致的。
如果满足假设1-3和假设4（2），
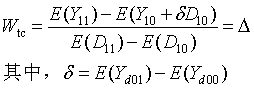
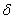表示对照组个体在D=d的状态下从T=0到T=1的结果变化。
*3.Wald-CIC*
*假设7：*“单调性以及时间与不可观测项无关”，要求了如G等在结果的效用方程（类似）中的不可观测项与时间无关，且结果对于T是严格递增的。
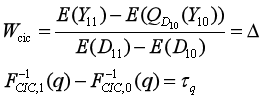
*4.如何选择统计量*
假设5的合理性会限制Wald-DID的适用性，Wald-TC和Wald-CIC的选择取决于假设4(2)和假设7。
如果处理组和对照组在第一阶段Y的分布存在较大差异，则Y的范围可能对Wald-TC的影响较大，而Wald-CIC对于Y的范围并不敏感，可以选择Wald-CIC
如果第一阶段Y的分布相近，Wald-TC更好，因为假设4（2）的限定仅针对Y的均值，但是假设7的限定对Y的分布提出要求。
*5.检验*
命令中会有对三个统计量的趋同性进行检验